Integrals and Infections
What does the subject you likely found most difficult in high school have to do with preventing about 887,000 deaths annually from viral infection? A lot, actually, because math — that frustratingly complex discipline — is the key to understanding the universe.
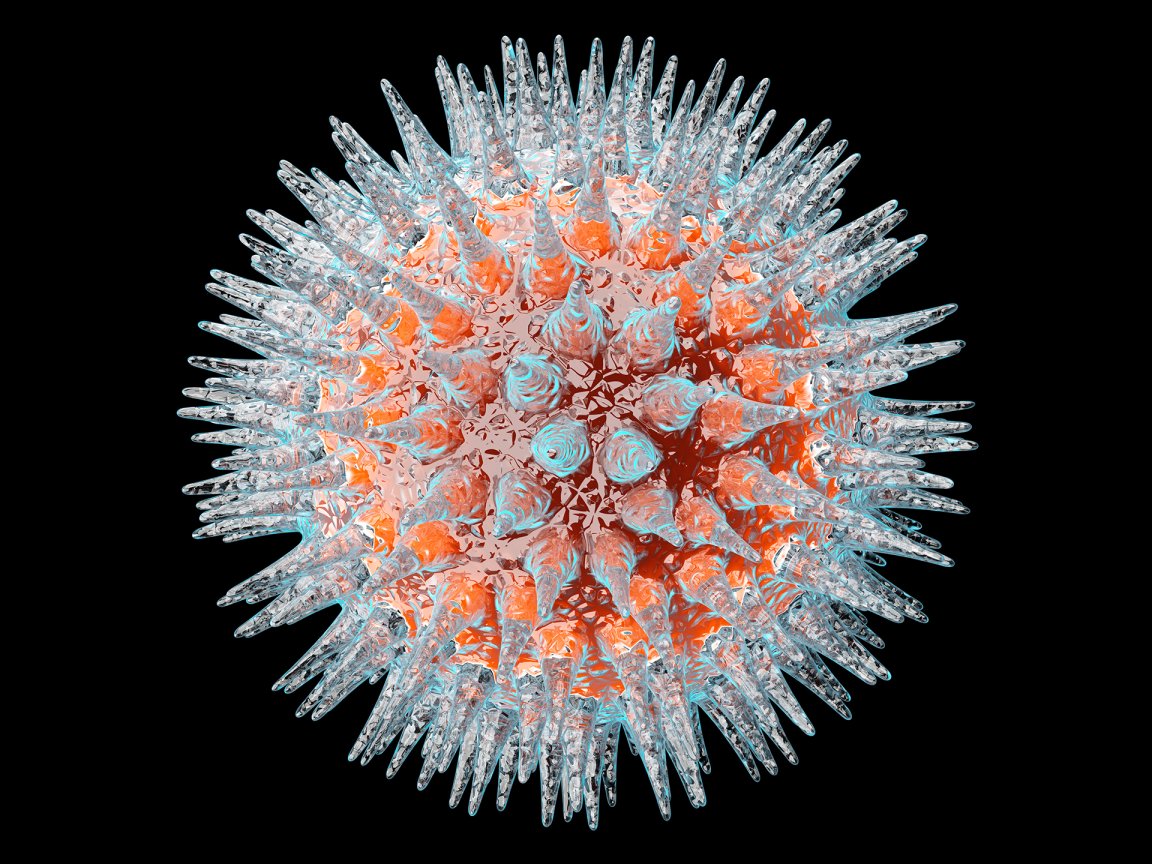
Numbers and equations help us to understand everything from patterns in plant life to the masses of distant stars. They have also helped us predict the shapes of tiny viruses — which can be too small to see by most microscopes.
Math is especially helpful in the case of viruses because the protein shells of most viruses are essentially geometric puzzles. The short genetic sequences of viruses code only a few distinctly shaped proteins, but these proteins can self-assemble into a variety of different 3D shapes. These structures are used to make the shell which encapsulates the viral genes, forming a virus that is ready to infect new organisms.

Scientists have been aware of virus self-assembly since the heyday of Watson and Crick, but how it occurs in many specific viruses remains a mystery that is still discussed. In fact, fifteen years ago, Reidun Twarock, a mathematician at the University of York, England, stumbled across a lecture about how viruses assemble a certain spherical shell, and she thought it related well to a project she was already working on. She decided to tackle the problem, and thus embarked on a new phase of her research.
“That snowballed,” Twarock said in an interview with Quanta Magazine. She realized her math could not only reveal how the viruses assemble, but how they infect cells and evolve. She began a collaboration with Peter Stockley, a professor of biological chemistry at the University of Leeds, England, and the marriage of math and biology turned out to be very fruitful.
“We really developed this integrative, interdisciplinary approach,” Twarock said in the interview, “where the math drives the biology, and the biology drives the math.”
Geometry Beats Germs
It was not long before the math drove the researchers to the conclusion that the order they were discovering on the viral surfaces must indicate that the virus’s genetics were playing a role — a physical one — in the protein shell’s assembly. After applying several mathematical theories to the problem, Twarock determined that the virus’s RNA was sticking to the proteins, helping them form the new virus.
The team applied this approach to viruses of special interest, reporting their findings about a common-cold virus this February in a Nature Communications study, and then about the HBV virus — the one that causes 887,000 deaths a year — this summer in a Nature Microbiology study.
And their research has not just gleaned academic insight into these viruses. “We’d like to vaccinate people against several hundred infections,” Stockley told Quanta Magazine. And the way they are perusing this goal is by exploring what could be a new class of vaccines.
There are currently two main types of approved vaccines — one that uses “dead” pathogens, which is not always as effective, and another that uses “live” but weakened pathogens, which causes stronger immunity, but also poses greater risks. However, the new kind of vaccine that Stockley proposes would use what math has revealed about viral assembly to engineer virus-like particles. They would be similar enough to the actual virus that they might be able to bring about the same immunity “live” viruses can — but without the risk, because they wouldn’t be able to infect cells.
Such a class of vaccines would not only be able to protect people from the HBV virus, but from a multitude of other viruses as well, adding to the millions of people that vaccines have already saved. And without the advanced math skills of people like Twarock, this kind of medicine would be impossible.