This paper is epic in both content and design. The physicists named the paper Traversable Achronal Retrograde Domains In Spacetime (go ahead and work out that acronym). It was authored by Ben Tippett and David Tsang (real physicists) who claim to work at the Gallifrey Polytechnic Institute and the Gallifrey Institute of Technology (unfortunately, not real institutions). Given the name of the paper and the names of their supposed institutions, I'm pretty sure Tippett and Tsang are fans of the fantastic Doctor Who program (clearly, there’s no point a being a grown-up scientist if you can’t have fun sometimes). In reality, Tsang is a theoretical astrophysicist who earned his degree at Cornell. He is currently at McGill University in Canada. Tippett is also a theoretical physicist and mathematician who currently teaches at the University of British Columbia.
OK, let's look at the actual paper. First things first. In case you don't know, spacetime geometry basically describes the structure of the fabric of our reality. This geometry essentially governs the nature of our universe. Spacetime in our universe, as far as we know, is constructed out of three dimensions of space and one dimension of time. The geometry of spacetime and the study of this structure is extremely complicated, and it is currently a hot area of research (as a result, there are many proposed models to describe this geometry, such as Euclidean and Minkowski space).
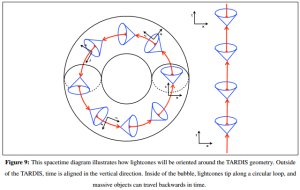
In order for a TARDIS to function, it needs to exist in a universe where the construction of closed timelike curves (CTCs) is possible. A closed timelike curve is defined by instances where the time dimension curves back on itself creating a closed loop. Hypothetically speaking, you could get in this loop (or build one around yourself) and travel forward and backwards in time at will.
The TARDIS proposed in Tippett and Tsang's paper would create one of these timelike curves (called a Traversable Achronal Retrograde Domain In Spacetime - or a TARDIS), and then move through time and space with an adventurous pilot, a daring companion, and enough Jelly Babies to go around (okay, maybe not all those things...but you get the idea).
As with any great adventure, there is always some danger and some limitations. To build a TARDIS bubble, the travelers would require the use of exotic matter - matter that has yet to be shown to exist in our universe; it would also have to violate classical mechanics. And that is the easy bit. Conquering this hurdle would allow for a TARDIS vehicle to travel in circles (in both time and space - but that's rather boring). To travel in other more complicated ways, we would have to cut two TARDIS bubbles and connect two ends from the two different bubbles. When you're watching the opening credits for Doctor Who, this mechanism is what you're watching (you're inside the time vortex/TARDIS bubble and, whenever the TARDIS changes directions, it has entered a different such bubble).
What's the catch (what's *another* catch)? When you connect two TARDIS bubbles, it's possible that you'll enter from one side, and exit into a universe made out of antimatter (I'm sorry. I'm so sorry).
The coolest thing about this TARDIS paper is The Blue Box White Paper, which is an explanation of the TARDIS paper written for laypeople by the original authors. The paper is easy to understand and filled with more Who references and analogies than I managed to cram into this article.
In the end, what can we say other that a straight line may be the shortest distance between two points, but it is by no means the most interesting. Geronimo!
Share This Article