Is Absolute Zero Absolute?

Right now, as I type this sentence, Earth's Northern Hemisphere is tilted away from the bright ball of light that is the Sun, and it’s cold here (relatively speaking). Humans have long  recorded and measured the temperature of their environment, and for good reason. Keeping constant watch on a thermometer helps us prepare for the potential dangers of cold weather. Take zero degrees Celsius, for instance. At such temperatures, water begins to freeze. In some cases, the pipes that the water runs through  malfunction, and then there's the various life-or-death afflictions that can be brought on by this cold temperature. However, zero degrees Celsius is pretty warm compared to zero degrees on the Fahrenheit scale (after all, water freezes at 32 F).

Yet, neither of these can compare to the temperature known as absolute zero.

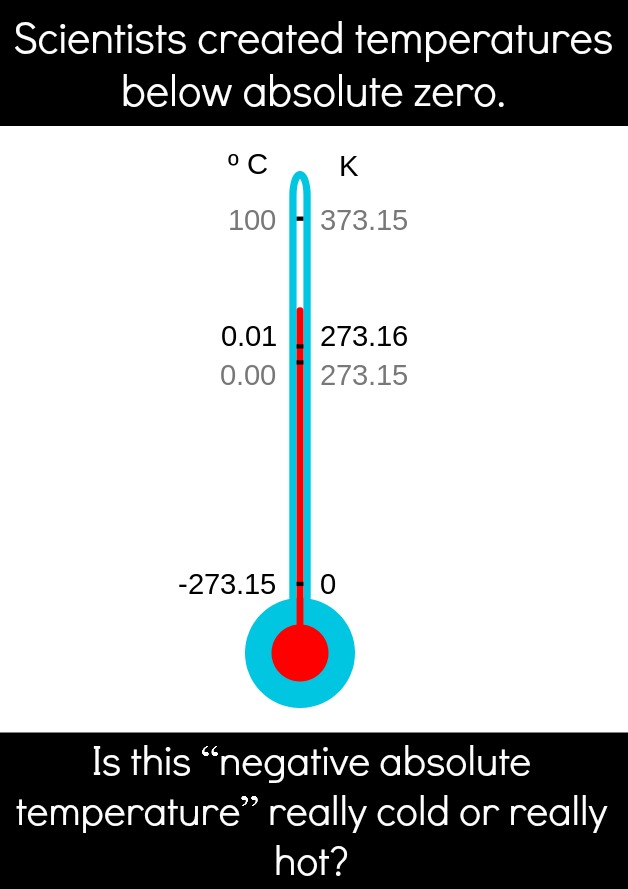
Absolute zero is the lowest possible temperature, which is reached at zero kelvin. To model how cold absolute zero is, think about this: Water freezes at 0 °C or 32 °F), which is 273 kelvins (not even close to absolute zero). In fact, absolute zero isn't reached until you hit−273 °C  or −459 °F (even empty space isn’t that cold; it sits at about 2.7 K, because of residual heat left over from the Big Bang).

So, what is absolute zero? In short, absolute zero is when all molecular movement stops. At this temperature, things aren't merely just frozen (or solid). Rather, this is the point at which entropy reaches its minimum value. If you don't know what "entropy" means, it refers to the amount of disorder in a system (a detailed description can be found here). In short, the higher your temperature, the higher your entropy. The lower your temperature, the lower your entropy. If you think about it, all temperature really means is how much all the atoms in a substance (liquid, gas, solid, or whatever) are moving. So as you put energy into a system, the atoms move around more, becoming more disordered, and bam! You have high(er) entropy.

Most of the time, absolute zero is absolute, unless you have a fancy lab and a lot of equipment. In that case, you can “flip” the temperature of a system, effectively making the temperature negative on the Kelvin scale. This seems impossible, right? How does one go beyond absolute zero? Through a very complicated process. And through this process, it seems we’ve changed everything we know about temperature and what it means to be cold.

You may be asking, “how do you get a temperature lower than the lowest?” The answer is, you make something very, very hot. At this point, we have to think of individual atoms. As you increase the average energy of a system (we’ll call it a gas), some of the atoms gain energy and occupy a higher energy state, while others occupy lower energy states. This makes the system more disordered (hence, higher entropy). In this example, the atoms are all spread out and have different energies and so on. The highest positive temperature means that the gas is as disordered as it can get, with atoms in every possible state. Now, imagine you keep adding energy to the gas, past maximum entropy. Even the lowest-energy atoms start to occupy higher energy states, until all the atoms are in a similar state (at a similar energy). That sounds a lot like low entropy to me (a more detailed description of the experiment can be found here).

For most of us, the aforementioned example makes little sense.. So, to get a full picture of the topic, let's visualize it using a graph, or even better, a picture. Imagine you have a group of particles that are very cold (low temperature aka not moving very much aka low entropy). These particles occupy a valley in our visual landscape of science. Now, as you add energy (heat) to the mix, the particles start to climb a mountain. Some of the particles zip right up the slope with youthful fervor, and some lag behind. Now we have higher entropy; our particles are farther apart, some are still in the valley, some are just leaving, while others are on their way right up the mountain. Over time, as we add more and more energy to the system, some particles will reach the top of the mountain, then some right behind, and others behind them, and so on. Now our particles are at every place on the mountain; no particle is near any other particle—it’s pure madness. We have reached maximum entropy in our system; the particles can’t spread out anymore, the temperature is infinitely hot, and the entire mountain is covered.

Now, we continue to add energy to this mountain, and as energy increases, the particles have no choice but to climb the mountain. Soon the particles form groups, steadily moving upwards and eventually the particles are at the peak, all together, all very excited. It seems now that our particles are very close to each other, very ordered – but still very energetic Our mountain once again has low entropy, but very, very high energy. Our particles are now occupying negative temperatures. Congratulations particles!

It is helpful to think of temperature not as a line, but as a circle: As your temperature reaches infinity, you loop right over to negative infinity, then down to negative absolute zero, and so on. It’s safe to say that this doesn’t happen in the natural world (as far as we know), but scientists have shown again and again that we can, in fact, surpass an infinitely hot temperature into negative absolute temperatures.

If disobeying the laws of physics isn’t exciting enough for you, negative absolute temperatures have even more to offer scientists. One exciting effect is that a gas cloud at negative absolute temperature could defy gravity and push against it (something matter doesn’t ordinarily do). Sub-absolute-zero atoms also have the interesting quality--they act like dark energy. Attractive atoms that would normally collapse into themselves are, instead, pushed outward and stabilized by the negative temperature, which could be very interesting for cosmologists studying the effects of dark energy and the expansion of the universe.

At any rate, always remember, when science gives you a rule or law, that’s really just an excuse to try to break it—that’s what science is all about, proving itself wrong, and this is a prime example of that.

As usual, a fun video explaining negative absolute temperatures:  here.