

Question asked by Robert: Are there any planets that do not actually orbit but are instead stationery relative to their parent stars? Is this scenario possible?
I’m going to say no because I think it’s the most correct answer to your question. But, I need to elaborate.
Firstly, if you have a two-object system, they actually ‘technically’ orbit each other. When you think of a binary system, you normally imagine two objects orbiting each other. Well, according to orbital mechanics, any two bodies in a stable orbit with each other orbit the barycentric coordinates (basically, the center of mass between the centers of the two bodies).
What does that mean? Basically, moons and planets, stars and planets, all orbit each other. As an example, this means the Earth orbits the moon and vice versa. Now, the question is where do you draw the line between what constitutes an object orbiting around another (such as the Earth-Moon system) or two objects orbiting around each other (Like a binary star system).
When one body is much more massive than the second body, the larger body will appear to wobble instead of orbiting around a seperate point – this is because the barycentric coordinates are within the larger body. Now, for some examples of what that means.
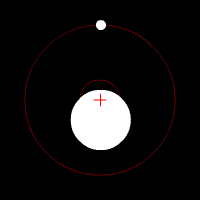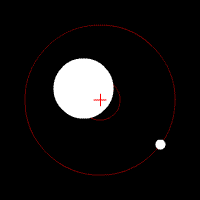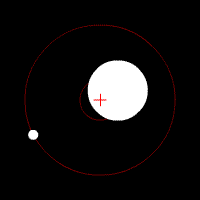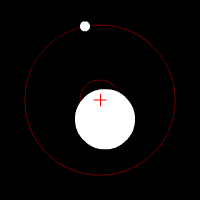
Lets use the Earth-Moon system as an example. Earth’s radius is 6,380 km, the Earth-Moon barycentric coordinates are 4,670 km above Earth’s center. This means these coordinates appear within the Earth (or, about 0.732 Earth’s radius) and the moon affectively orbits around the Earth.

Using the Earth-Sun system as an example, these baycentric coordinates are located about 449 km from the center of the sun. This obviously means the Earth orbits around the Sun.
Of the planets in our solar system, Jupiter has the greatest affect on the sun since the barycenter coordinates for this system is 1.07 the radius of the Sun (meaning the barycenter is just above the surface of the Sun). Technically, it could be said that Jupiter and the Sun orbit each other (in the traditional binary-system sense) save for the fact that Jupiter is a planet and the Sun is a star. This means that the Sun-Jupiter system isn’t a binary system since a binary system consists of tow objects that are very similar.
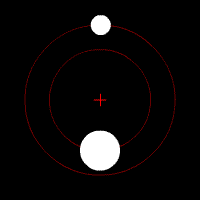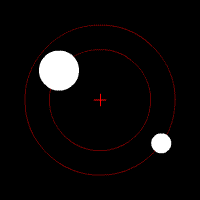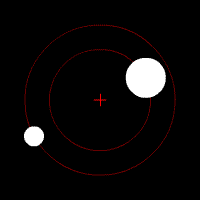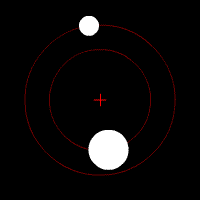
To give an example of what a binary system looks like, I’ll turn to the Pluto-Charon system. . Here, we find the barycenter is 1.83 the radius of Pluto. In addition, if you look at the orbits of Pluto’s four other moons, you’ll find that they orbit Pluto-Charon instead of limiting themselves to Pluto. Because of this, Pluto and Charon were actually considered a double planet before Pluto’s reclassification in 2006. Especially after the AIU reclassified Pluto in 2006, they didn’t want to make an official decision on Pluto-Charon’s dwarf planet-moon/dwarf-planet binary status and opted to let public opinion calm down over Pluto’s reclassification instead (after all, if an object has a moon, it’s more important, right?). But, that is a post for another time.
Of course, all of this is dependent on what you mean by your use of the phrase ‘relative to the parent star’, but either way I’d have to lean towards no because a planet is much, much, much smaller than a star. For a planet to be of an appropriate size to force a star to orbit around it, the planet would be massive enough to start nuclear fusion at it’s core and ignite – or, in other words, the planet wouldn’t be a planet, it would be a star. The closest you could come to your scenario is to pair a large planet with a small star (such as Jupiter (1 Jupiter Mass) with the brown dwarf OTS 44 (at 15 Jupiter masses, it’s the smallest ‘star’ found to date) or the red dwarf Gliese 570D (at 52 Jupiter masses, it’s the smallest ‘ignited’ star discovered to date). The Sun, for reference, is 1042 Jupiter masses.
Of course, in whichever case you decide to partake, the best you could manage is a system that has a ‘binary’ orbit (meaning the barycentric coordinate isn’t found within either body) but the system wouldn’t be a binary system since both objects are different from one another and you couldn’t come up with a case where a star is orbiting around a planet because they are simply too massive. (after all, for that to happen, the planet must be more massive than the star, at maximum, they could be nearly equal – such as a very large gas giant just shy of being a brown dwarf and a very small brown dwarf just shy of being a gas giant).