
Nature’s Simple Complexity
Deep learning can be understood as modeling high-level abstractions using data and a set of algorithms, with a deep graph and multiple processing layers of linear and non-linear equations. While it is largely a mathematical tool, the things that deep neural networks can do have surprised mathematicians. How can networks arranged in layers be quick to perform human tasks like face and object recognition if it has to go through layers of computations? This has perplexed mathematicians for sometime.
However, what mathematics cannot makes sense of, physics explains simply.
According to Henry Lin of Harvard University and Max Tegmark at MIT, the answer lies in understanding the nature of the universe, for which physics is the best tool.
Mathematically, object recognition goes through multiple possibilities. As explained by MIT Technology Review, to determine whether a megabit greyscale image shows a cat or a dog, it has to go through 2561000000 possible images. Not only that, it has to compute whether each shows a cat or a dog. Neural networks do this, however, with ease.
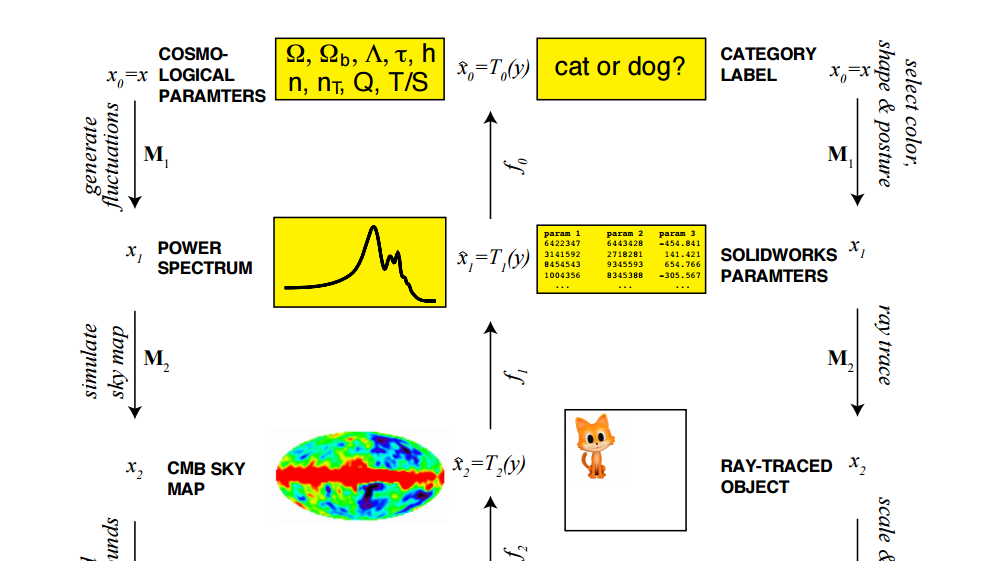
Neural networks approximate complex mathematical functions with simpler ones. In theory, this mean that neural networks have to go through a magnitude of mathematical functions more than what is possible for them to approximate. Lin and Tegmark believe that it doesn’t have to go through all the probability of mathematical functions but just a tiny subset of them.
And this is because the universe, in all its complexity, is governed by a tiny subset of all possible functions. Mathematically, the laws of physics can be described using functions with a set of simple properties. Neural networks approximate how nature works.
Tapping Into Nature’s Laws
“For reasons that are still not fully understood, our universe can be accurately described by polynomial Hamiltonians of low order,” Lin and Tegmark observe.
Furthermore, the laws of physics are usually symmetrical when rotated or translated, which simplifies approximating the process of object recognition.
Neural networks tap into another property of the universe in simplifying its tasks. Lin and Tegmark explain: “Elementary particles form atoms which in turn form molecules, cells, organisms, planets, solar systems, galaxies, etc.” Complex structures are but a sequence of simpler steps. And because neural networks are composed of layers of code, these can approximate the steps in the sequence of causes in nature. The higher the layer, the more data is contained.
So Lin and Tegmark conclude: “We have shown that the success of deep and cheap learning depends not only on mathematics but also on physics, which favors certain classes of exceptionally simple probability distributions that deep learning is uniquely suited to model.”
With this, deep learning is geared to advance even more, with the help of mathematicians, of course.